The following is a simplification of procedures for predicting well performance. This discussion assumes a flow efficiency of one. A damaged well or other factors will effect the flow efficiency and could change the well's productivity.
Productivity Index
When the well flowing pressure (Pwf) is greater than bubble -point pressure (Pb), the fluid flow is similar to single phase flow, and the inflow performance curve is a straight line with slope J, as given by the productivity index, PI:
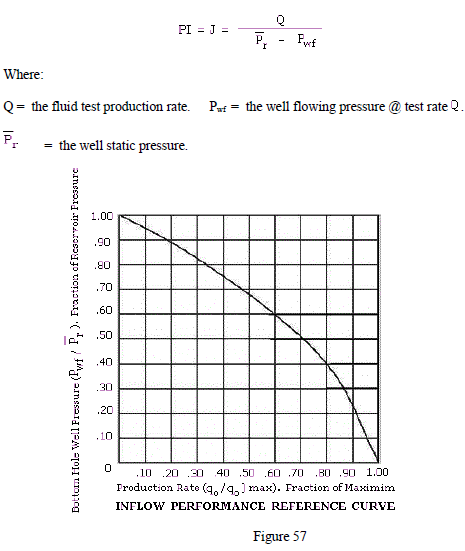
Inflow Performance Relationship

This relationship was first used by W.E. Gilbert1 and further developed by J.V. Vogel2. Vogel developed a dimensionless reference curve that can be used to determine the IPR curve for a particular well.
Formation Damage and skin factor
Wellbore damage occurs when filtrate (liquid) or solids from drilling mud or completion fluids interact or plug the formation near the wellbore. Water in the filtrate can swell the clays or fines from the solids can plug the pore throats. Both result in a reduction in the size of the flow channels and hence a reduction in the near wellbore permeability. This is referred to as skin damage. The skin factor is a numerical representation of skin damage. The additional pressure drop in the near wellbore due to skin is called Δpskin.
Flow Efficiency
The Vogel equation was modified by Standing, who represented the Vogel Equation as the situation when the Skin Factor is zero. The flow efficiency can be estimated as:
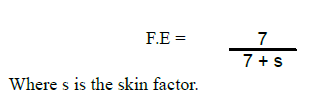
If the skin factor is positive (s>0), then the Flow Efficiency is less than 1 indicating that the well is damaged. If the skin factor is negative (s<0), then the Flow Efficiency is greater than 1 indicating that well is stimulated.

For the well represented in the graph above, the unstimulated well will produce at a rate of approx. 1,750 bopd for a flowing bottomhole pressure of 1,000 psia, while the production rate for the same flowing bottomhole pressure will be approx. 2,400 bopd, an increase of 650 bopd.
Darcy Equation for Radial Flow
Previously we looked at the Darcy Equation for linear flow for incompressible fluids. However, radial flow exists in a reservoir (flow from all directions in a radial pattern as shown below).

Darcy developed an equation for radial flow, which estimates the radial fluid flow thropugh porous media:

From the above equation, we can see that a positive skin factor (s>0) will result in a reduction in the well’s oil rate, while a negative skin factor rill result in an increased flow rate in the well. This forms the basis for well stimulation.




